Guía práctica para el diseño de un muro de contención: paso a paso con ejemplo

·9 ene 2025

Cover for Guía práctica para el diseño de un muro de contención: paso a paso con ejemplo

Calcula tus muros de contención con Rischio.io

Rischio.io es una plataforma de cálculo en ingeniería civil que provee la herramienta muro de contención, que permite el análisis y diseño de todo tipo de muros de contención. Sus resultados son presentados de manera transparente y encontrarás todos los parámetros utilizados para llegar a la solución presentada.

¡Prueba ahora nuestra plataforma! Regístrate gratis

Convenciones de un muro de contención

Un muro de contención consta de múltiples elementos o partes que se presentan en el esquema a continuación.

Esquema de un muro de contención

Estos elementos son:

Pantalla o muro: Es el elemento estructural principal del muro de contención, encargado de resistir los empujes del suelo retenido. Puede ser de concreto armado, mampostería u otros materiales estructurales.
Cara posterior: Es la parte del muro que está en contacto con el suelo retenido y soporta la presión lateral del terreno.
Cara frontal: Es la parte expuesta del muro, generalmente visible y sin contacto directo con el relleno.
Contrafuerte: Son elementos verticales ubicados en la cara frontal del muro y perpendiculares a este. Su función es reforzar la estructura, aumentando la rigidez y reduciendo el momento flector en la base.
Zapata: Es la base del muro de contención, encargada de distribuir las cargas hacia el suelo de cimentación para garantizar la estabilidad estructural.
Puntera: Es la parte delantera de la zapata, que se proyecta hacia la cara frontal del muro. Ayuda a mejorar la estabilidad contra el vuelco.
Llave: Es un elemento que sobresale en la parte inferior de la zapata, generalmente ubicado en la base del muro. Su función principal es incrementar la resistencia al deslizamiento mediante la generación de empuje pasivo en el suelo.
Talón: Es la parte trasera de la zapata que se extiende hacia el suelo retenido, proporcionando estabilidad adicional al muro.
Relleno: Es el material granular o suelo colocado detrás del muro de contención, sobre el talón. Su objetivo es reducir las presiones laterales y facilitar el drenaje del agua.

¿Qué se analiza al momento de diseñar un muro de contención?

Mecanismos de falla de un muro de contención

Al diseñar un muro de contención se deben analizar tres posibles mecanismos de falla:

Falla por volcamiento: cuando los momentos actuantes exceden los momentos resistentes.
Falla por deslizamiento: cuando as fuerzas horizontales actuantes exceden las fuerzas horizontales resistentes.
Falla por capacidad portante: cuando las fuerzas verticales exceden la capacidad portante del suelo.

Guía paso a paso

Conociendo los elementos que conforman un muro de contención y los mecanismos de falla que debemos considerar, presentamos el paso a paso para diseñar tus muros de contención.

1. Cálculo de fuerzas actuantes sobre el muro

Fuerzas actuantes sobre el muro

Las fuerzas actuantes en un muro de contención corresponden a:

El peso propio de la estructura.
El peso del suelo sobre el talón, incluyendo la cuña superior cuando el relleno está inclinado.
El empuje activo del relleno.
El empuje pasivo del suelo correspondiente a la profundidad de desplante en la cara frontal (opcional).

2. Factor de seguridad para volcamiento

Para el cálculo del factor de seguridad para volcamiento es necesario calcular los momentos actuantes sobre el muro con respecto a la base de la puntera.

Estos momentos deben clasificarse en dos grupos:

Momentos volcantes: son aquellos que desestabilizan a la estructura, generalmente es la componente horizontal del empuje activo.

\sum M_O = P_H \cdot \frac{H'}{3}

Momentos resistentes: son aquellos que estabilizan a la estructura, generalmente es el peso propio de la estructura y el peso del suelo sobre el talón.

\sum M_R = M_1 + M_2 + M_3 + M_4 + M_5 + P_V \cdot B

Ten en cuenta que las ecuaciones presentadas corresponden al caso propuesto en este artículo y deben ser adaptadas según las condiciones de tus proyectos, que puede incluir múltiples tipos de suelo en el relleno, un muro de otra tipología, entre otros.

Una vez calculados los momentos volcantes y los momentos resistentes, se debe calcular el factor de seguridad para falla por volcamiento.

FS_{\text{volcamiento}} = \frac{\sum M_R}{\sum M_O} \geq 2.0

Usualmente este factor de seguridad se espera que sea mayor a 2.0, sin embargo, este valor puede variar según la normatividad y los requerimientos del proyecto.

También, se debe verificar que la excentricidad de las cargas aplicadas sea inferior a $B/6$ para evitar tensiones en la base del muro, que generarían condiciones inseguras en el muro.

e_{max} = \frac{B}{2} - \frac{\sum M_R - \sum M_O}{\sum V} \leq \frac{B}{6}

Donde $\sum V$ corresponde a la suma de las fuerzas verticales, que usualmente incluyen el peso de la estructura, el peso del suelo sobre el talón y la componente vertical del empuje activo.

3. Factor de seguridad para deslizamiento

El cálculo del factor de seguridad para deslizamiento requiere calcular las fuerzas horizontales desestabilizantes y las fuerzas horizontales estabilidantes.

Fuerzas desestabilizantes: Generalmente incluye el empuje activo del suelo y la presión hidrostática, según sea la condición del muro.

\sum F_S = P_H

Fuerzas estabilizantes: Corresponde a la resistencia en la base del muro y al empuje pasivo del suelo en la cara frontal (opcional).

\sum F_R = \sum V \cdot \tan \delta + B \cdot c'_a + P_p

Donde:

$\delta$ corresponde al ángulo de fricción entre el muro y el suelo. Usualmente se utiliza $\delta=\frac{2}{3} \phi'_2$
$c'_a$ corresponde a la adhesión entre el muro y el suelo. Usualmente se utiliza $c'_a=\frac{2}{3} c'_2$

Con estas variables, se realiza el cálculo del factor de seguridad por deslizamiento.

FS_{\text{deslizamiento}} = \frac{\sum F_R}{\sum F_S} \geq 1.5

Usualmente este factor de seguridad se espera que sea mayor a 1.5, sin embargo, este valor puede variar según la normatividad y los requerimientos del proyecto.

4. Factor de seguridad para capacidad portante

Por último, para calcular el factor de seguridad por capacidad portante requerimos calcular la presión vertical máxima aplicada sobre el suelo y su capacidad portante.

Presión vertical máxima: al tratarse de una carga excéntrica, la distribución de la presión en el suelo no será uniforme. La presión máxima se define como:

P_{max} = \frac{\sum V}{B} \left( 1 + \frac{6 \cdot e}{B} \right)

Distribución de presión en la base del muro

Y una verificación adicional es que las presiones siempre deben ser positivas, es decir, que no se generen tensiones en el suelo.

P_{min} = \frac{\sum V}{B} \left( 1 - \frac{6 \cdot e}{B} \right) > 0

Capacidad portante: en este caso, se modela el muro de contención como si se tratara de una zapata continua y su capacidad portante se calculará usando la Ecuación General de Capacidad de Carga o ecuación de Meyerhof.

q_{ult} = c_2 N_c F_{cd} F_{ci} + q N_q F_{qd} F_{qi} + \frac{1}{2} B' N_\gamma F_{\gamma d} F_{\gamma i}

Donde:

$N_c$ , $N_q$ , $N_\gamma$ son los factores de capacidad de carga de la ecuación de Meyerhof.
$q = \gamma_2 \cdot Df$ . Este valor puede verse afectado por el nivel freático en la cara frontal del muro.
$B' = B - 2e$ . En algunos casos, la excentricidad puede ser negativa, por lo cual se sugiere tomar su valor absoluto para este cálculo.
Factores de profundidad

F_{qd} = 1+2 \tan \phi_2 (1-\sin \phi_2)^2 \left( \frac{Df}{B'} \right)

F_{cd} = F_{qd} - \frac{1+F_{qd}}{N_c \tan \phi'_2}

F_{\gamma d} = 1

Factores de inclinación

F_{ci} = F_{qi} = \left( 1- \frac{\psi}{90°}\right)^2

F_{\gamma i} = \left( 1- \frac{\psi}{\phi'_2}\right)^2

\psi = \tan^{-1} \left(\frac{P_H}{\sum V}\right)

Los factores de forma ( $F_{cs}$ , $F_{qs}$ y $F_{\gamma s}$ ) no se incluyen en esta ecuación ya que al tratarse de una zapata continua, estos tienden a cero.

Se debe prestar atención al momento de seleccionar los parámetros del suelo correspondientes a cohesión, ángulo de fricción y peso específico, ya que son los del suelo de fundación y no los del relleno.

Una vez se calcula la capacidad portante y la presión máxima, se debe calcular el factor de seguridad.

FS_{\text{capacidad portante}} = \frac{q_{ult}}{P_{max}} \geq 3.0

Usualmente este factor de seguridad se espera que sea mayor a 3.0, sin embargo, este valor puede variar según la normatividad y los requerimientos del proyecto.

Recomendaciones si alguno de los factores de seguridad no cumple

Encontraremos situaciones en que los muros de contención no cumplen algunos de los factores de seguridad o condiciones mencionadas anteriormente, por lo cual nuestro diseño debe ser reevaluado. Es importante entender las razones por las cuales no se cumplen estos factores para tomar decisiones que optimicen el uso de recursos en los proyectos.

Algunas de las recomendaciones para mejorar la estabilidad de los muros de contención son:

Incrementar la base del muro: incrementa los momentos resistentes, la resistencia en la base y la capacidad portante.
Reducir la altura del muro: disminuye el empuje activo.
Cambiar el material del relleno por uno más ligero: reduce el empuje activo.
Cambiar el tipo de muro: la geometría influye especialmente en los momentos resistentes.
Controlar el nivel freático del relleno: siempre se debe hacer un manejo adecuado de las aguas en la cara posterior del muro, por lo cual es importante contar con un buen sistema de drenaje que impida su acumulación.

Ejemplo de cálculo

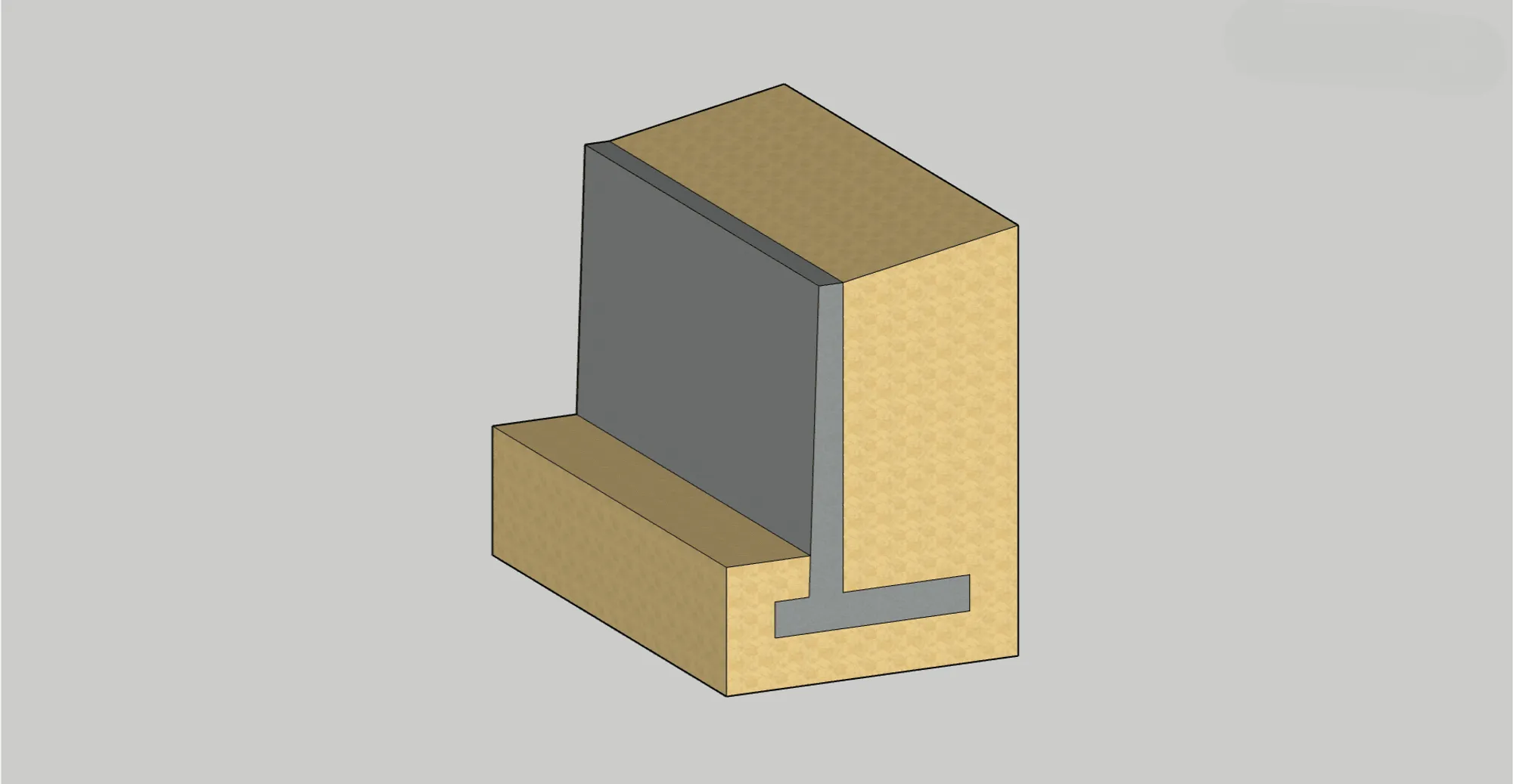
Calcula los factores de seguridad de volcamiento, deslizamiento y capacidad portante para el muro en la siguiente figura.

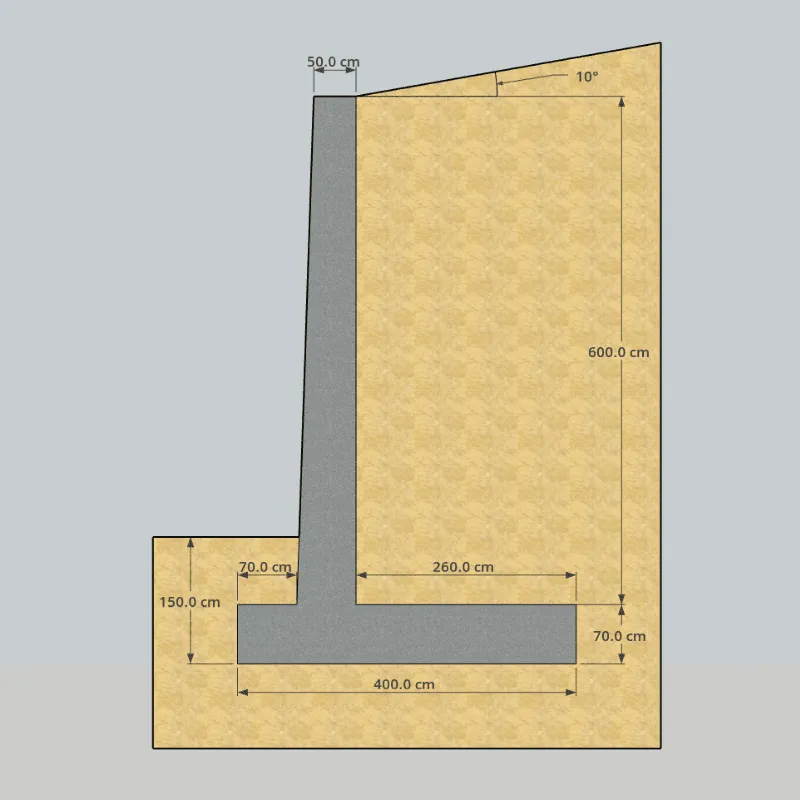
Ejemplo de cálculo de muro de contención

1. Identificar los elementos que conforman el muro y las fuerzas a las que está sujeta

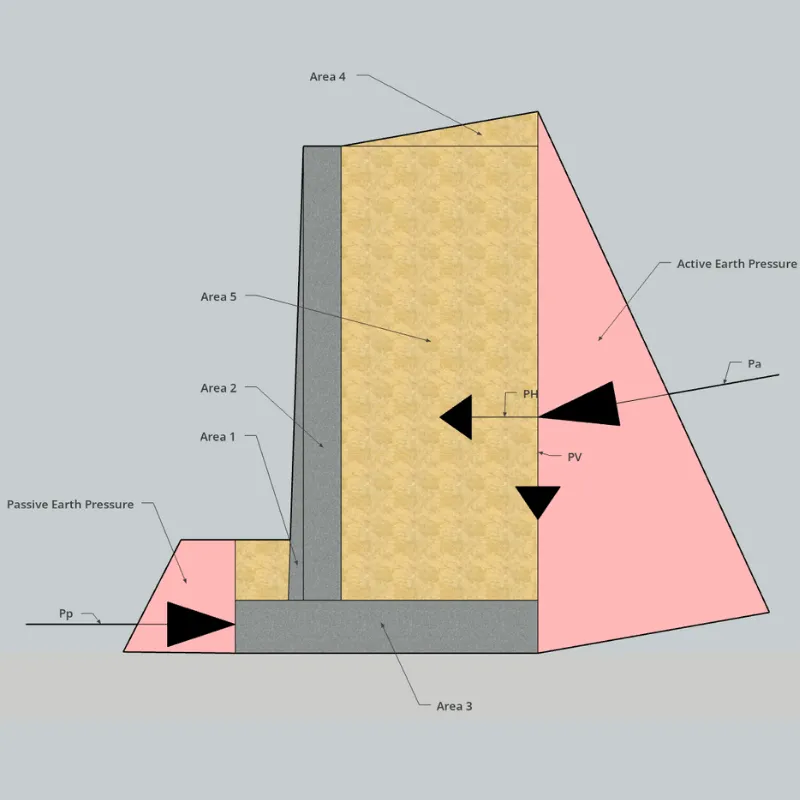
Ejemplo: fuerzas aplicadas sobre el muro

En este caso se divide la estructura en las figuras 1, 2 y 3. El suelo sobre el talón corresponde a las figuras 4 y 5. Y por último, se identifica el empuje activo ( $P_a$ ) junto con sus componentes horizontal ( $P_H$ ) y vertical ( $P_V$ ).

También, se calcula el valor de H’.

\begin{aligned} H' &= H + \Delta x \tan{\alpha} &= 6 + 0.5 \tan{10°} \\ &= 6.09 \text{m} \end{aligned}

2. Calcular el empuje activo y empuje pasivo

Primero debemos calcular el coeficiente de empuje activo del relleno.

\begin{aligned} K_{a} &= \tan^2\left( 45° - \frac{\phi'_1}{2} \right)\\ &= \tan^2\left( 45° - \frac{30°}{2} \right) \\ &= 0.333 \end{aligned}

El empuje activo lo calculamos rápidamente ya que se trata de un área triangular.

\begin{aligned} P_a &= (\gamma_1 \cdot H') \cdot K_a \cdot \frac{H'}{2} \\ &= (18 \cdot 6.09) \cdot 0.333 \cdot \frac{6.09}{2}\\ &= 111.15 \text{kN} \end{aligned}

Luego, se calcula el coeficiente de empuje pasivo.

\begin{aligned} K_{p} &= \tan^2\left( 45° + \frac{\phi'_2}{2} \right)\\ &= \tan^2\left( 45° + \frac{20°}{2} \right) \\ &= 2.04 \end{aligned}

Por su parte, el empuje pasivo se trata de un trapecio, el cual definimos a continuación.

\begin{aligned} \text{Base superior} &= 2 \cdot c'_2 \cdot \sqrt{K_p} \\ &= 2 \cdot 10 \cdot \sqrt{2.04} \\ &= 28.57 \text{kPa} \end{aligned}

\begin{aligned} \text{Base inferior} &= \gamma_2 \cdot D_f \cdot K_p + 2 \cdot c'_2 \cdot \sqrt{K_p} \\ &= 18.5 \cdot 1.5 \cdot 2.04 + 2 \cdot 10 \cdot \sqrt{2.04} \\ &= 85.18 \text{kPa} \end{aligned}

Ahora, calculamos el área del trapecio para obtener el empuje pasivo.

\begin{aligned} P_p &= \frac{\text{Base superior} + \text{Base inferior}}{2} D_f \\ &= \frac{28.57 + 85.18}{2} 1.5 \\ &= 85.31 \text{kPa} \end{aligned}

3. Calcular las fuerzas y momentos aplicados sobre el muro

Una vez obtenidas las fuerzas, debemos calcular el peso de cada elemento, su centroide respecto a la puntera y con ello encontraremos la suma de las fuerzas verticales ( $\sum V$ ), y los momentos volcantes ( $\sum M_O$ ) y resistentes ( $\sum M_R$ ).

Elemento	Área	Peso-Fuerza vertical	Fuerza horizontal	$\bar{x}$	$\bar{z}$	$M_R$	$M_O$
1	2.5	60	*	1.16	*	69.6	*
2	5.0	120	*	2	*	240	*
3	3.0	72	*	1.5	*	108	*
4	0.045	0.81	*	2.83	*	2.29	*
5	2.5	45	*	2,75	*	123.75	*
$P_H$	*	*	109.46	*	2.03	*	222.2
$P_V$	*	19.30	*	3	*	57.9	*
			$\sum V = 317.11$			$\sum M_R = 601.54$	$\sum M_O = 222.2$

Con estos resultados, el camino para calcular el factor de seguridad por volcamiento y deslizamiento se encuentra despejado.

4. Calcular el factor de seguridad por volcamiento y la excentricidad

Siguiendo la fórmula presentada anteriormente, calculamos el factor de seguridad.

\begin{aligned} FS_{\text{volcamiento}} &= \frac{\sum M_R}{\sum M_O} \geq 2.0\\ &= \frac{601.54}{222.2} \geq 2.0\\ &= 2.70 \geq 2.0 \end{aligned}

Se cumple el requerimiento de factor de seguridad.

Por otro lado, la verificación de excentricidad.

\begin{aligned} e_{max} &= \frac{B}{2} - \frac{\sum M_R - \sum M_O}{\sum V} \leq \frac{B}{6}\\ &= \frac{3}{2} - \frac{601.54 - 222.2}{317.11} \leq \frac{3}{6} \\ &= 0.304 \leq 0.5 \end{aligned}

Se cumple el requerimiento de excentricidad.

5. Calcular el factor de seguridad por deslizamiento

Aplicando la ecuación presentada.

\begin{aligned} FS_{\text{deslizamiento}} &= \frac{\sum V \cdot \tan \delta + B \cdot c'_a + P_p}{P_H} \geq 1.5 \\ &= \frac{317.11 \cdot \tan 13.33° + 3 \cdot 6.66 + 85.31}{109.46} \geq 1.5 \\ &= 1.65 \geq 1.5 \\ \end{aligned}

Cumple el requerimiento de factor de seguridad.

6. Calcular el factor de seguridad por capacidad portante

Hemos llegado a la última verificación, para la cual también haremos uso de los valores calculados en el paso 3.

Empezamos calculando la presión máxima sobre el suelo.

\begin{aligned} P_{max} &= \frac{\sum V}{B} \left( 1 + \frac{6 \cdot e}{B} \right) \\ &= \frac{317.11}{3} \left( 1 + \frac{6 \cdot 0.304}{3} \right) \\ &= 169.97 \text{kPa} \end{aligned}

Ahora, verificamos que la presión mínima sea positiva para evitar tensiones en el suelo.

\begin{aligned} P_{min} &= \frac{\sum V}{B} \left( 1 - \frac{6 \cdot e}{B} \right) > 0 \\ &= \frac{317.11}{3} \left( 1 - \frac{6 \cdot 0.304}{3} \right) > 0 \\ &= 41.44 \text{kPa} \end{aligned}

La verificación es correcta.

Con esto ya contamos con el denominador del factor de seguridad, solo nos queda calcular la capacidad portante.

Empezamos con los factores de capacidad de carga de la Ecuación de Meyerhof.

N_c = 14.83

N_q = 6.4

N_\gamma = 5.38

Continuamos con la sobrecarga y el ancho efectivo de la zapata.

\begin{aligned} q &= \gamma_2 \cdot Df \\ &= 18.5 \cdot 1.5 \\ &= 27.75 \text{kPa} \end{aligned}

\begin{aligned} B' &= B - 2e\\ &= 3 - 2 \cdot 0.304\\ &= 2.39 \text{m} \end{aligned}

Luego con los factores de profundidad.

\begin{aligned} F_{qd} &= 1+2 \tan \phi_2 (1-\sin \phi_2)^2 \left( \frac{Df}{B} \right)\\ &= 1+2 \tan 20° (1-\sin 20°)^2 \left( \frac{1.5}{3} \right)\\ &= 1.158 \end{aligned}

\begin{aligned} F_{cd} &= F_{qd} - \frac{1+F_{qd}}{N_c \tan \phi'_2} \\ &= 1.158 - \frac{1+1.158}{14.83 \tan 20°} \\ &= 0.758 \end{aligned}

\begin{aligned} F_{\gamma d} &= 1 \end{aligned}

Y por último los factores de inclinación.

\begin{aligned} \psi &= \tan^{-1} \left(\frac{P_H}{\sum V}\right)\\ &= \tan^{-1} \left(\frac{103.46}{317.11}\right)\\ &= 18.07° \end{aligned}

\begin{aligned} F_{ci} = F_{qi} &= \left( 1- \frac{\psi}{90°}\right)^2 \\ &= \left( 1- \frac{18.07°}{90°}\right)^2 \\ &= 0.639 \end{aligned}

\begin{aligned} F_{\gamma i} &= \left( 1- \frac{\psi}{\phi'_2}\right)^2 \\ &= \left( 1- \frac{18.07°}{20°}\right)^2 \\ &\approx 0 \end{aligned}

Con estos valores ya podemos calcular la capacidad portante del suelo.

\begin{aligned} q_{ult} &= c_2 \cdot N_c \cdot F_{cd} \cdot F_{ci} + q \cdot N_q \cdot F_{qd} \cdot F_{qi} + \frac{1}{2} \cdot B' \cdot N_\gamma \cdot F_{\gamma d} \cdot F_{\gamma i} \\ &= 10 \cdot 14.83 \cdot 0.758 \cdot 0.639 + 27.75 \cdot 6.4 \cdot 1.158 \cdot 0.639 + 0 \\ &= 203.25 \text{kPa} \end{aligned}

Y finalizamos calculando el factor de seguridad.

\begin{aligned} FS_{\text{capacidad portante}} &= \frac{q_{ult}}{P_{max}} \geq 3.0 \\ &= \frac{203.25}{169.97} \geq 3.0\\ &= 1.19 \geq 3.0 \end{aligned}

En este caso no se cumple el requerimiento de factor de seguridad, por lo cual es necesario rediseñarlo según las indicaciones dadas en esta guía y volver a calcularlo. Un buen punto de partida puede ser aumentar el ancho de la base del muro.

Referencias

Das, B. M., & Sivakugan, N. (2018). Principles of Foundation Engineering.

Volver a todas las entradas