Ingresar Regístrate gratis
Muros De Contencion

Rankine vs Coulomb para el cálculo del empuje lateral del suelo

Andrés Gracia avatar
Andrés Gracia
·
Cover for Rankine vs Coulomb para el cálculo del empuje lateral del suelo

Calcula tus muros de contención con Rischio.io

Rischio.io es una plataforma de cálculo en ingeniería civil que provee la herramienta muro de contención, que permite el análisis y diseño de todo tipo de muros de contención. Sus resultados son presentados de manera transparente y encontrarás todos los parámetros utilizados para llegar a la solución presentada.

¡Prueba ahora nuestra plataforma! Regístrate gratis

Empuje lateral del suelo

El empuje lateral del suelo es la presión que estos ejercen sobre las estructuras con las que interactúan, principalmente de estructuras de contención.

En el caso del empuje activo y empuje pasivo, existen dos teorías para su cálculo: la teoría de Rankine y la teoría de Coulomb. Cada una de estas teorías cuenta con distintas hipótesis que explicaremos a continuación.

Teoría de empuje lateral del suelo de Rankine

El ingeniero escocés William Rankine desarrolló en 1857 una teoría para calcular el empuje lateral del suelo activo y pasivo en muros de contención. Para esta formulación, Rankine tuvo en cuenta las siguientes hipótesis:

  • La cara posterior del muro es vertical.
  • El material de relleno tiene una superficie horizontal.
  • No hay fricción entre el muro y el relleno.

La formulación de Rankine está basada en la representación de las condiciones de esfuerzo al momento de la falla. De esta manera, el empuje activo de Rankine fue definido como:

σa′=σ0′tan⁡2(45°−ϕ′2)−2⋅c′tan⁡(45°−ϕ′2)=σ0′Ka−2⋅c′Ka\begin{aligned} \sigma'_a &= \sigma'_0 \tan^2\left(45° - \frac{\phi'}{2}\right) - 2 \cdot c' \tan\left(45° - \frac{\phi'}{2}\right)\\ &= \sigma'_0 K_a - 2 \cdot c' \sqrt{K_a} \end{aligned}

Donde:

  • σ0′\sigma'_0 es el esfuerzo efectivo vertical.
  • ϕ′\phi' es el ángulo de fricción del relleno.
  • c′c' es la cohesión del relleno.
  • KaK_a es el coeficiente de empuje activo del suelo.

Distribución del empuje activo de Rankine

Por su parte, el empuje pasivo se describe con la siguiente ecuación:

σp′=σ0′tan⁡2(45°+ϕ′2)+2⋅c′tan⁡(45°+ϕ′2)=σ0′Kp+2⋅c′Kp\begin{aligned} \sigma'_p &= \sigma'_0 \tan^2\left(45° + \frac{\phi'}{2}\right) + 2 \cdot c' \tan\left(45° + \frac{\phi'}{2}\right)\\ &= \sigma'_0 K_p + 2 \cdot c' \sqrt{K_p} \end{aligned}

Donde:

  • KpK_p es el coeficiente de empuje pasivo del suelo.

Distribución del empuje pasivo de Rankine

Es fundamental considerar las constantes 2cKa2c \sqrt{K_a} y 2cKp2c \sqrt{K_p}, ya que influyen en la distribución del empuje lateral activo y pasivo sobre el muro. En el caso del empuje activo, pueden generar zonas de presión negativa, mientras que en el empuje pasivo, la distribución de esfuerzos comienza con un valor positivo, lo que incrementa la fuerza pasiva resultante.

Otro caso para analizar es cuando hay una sobrecarga en la superficie del relleno, para lo cual consideraremos dos escenarios:

  • La sobrecarga se distribuye uniformemente sobre el relleno. En este caso, el esfuerzo efectivo vertical se incrementa uniformemente sobre toda la altura del muro.
σa′=(σ0′+q)Ka−2⋅cKa\sigma'_a = (\sigma'_0 + q) K_a - 2 \cdot c \sqrt{K_a} σp′=(σ0′+q)Kp+2⋅cKp\sigma'_p = (\sigma'_0 + q) K_p + 2 \cdot c \sqrt{K_p}

Sobrecarga uniforme

  • La sobrecarga es una franja sobre el relleno. Esta situación hace que el incremento de la distribución no sea uniforme sino que sea descrito por la siguiente ecuación que depende de la profundidad.
Δσh′=2qπ(β−sin⁡βcos⁡2α)\Delta \sigma'_h = \frac{2q}{\pi} (\beta - \sin\beta \cos 2\alpha)

Sobrecarga en franja

Por último, analicemos el caso de un relleno con superficie inclinada. En esta situación, el empuje lateral del suelo no se distribuye en dirección horizontal, sino que sigue la misma inclinación del terreno. Las ecuaciones a emplear en este caso son:

Ka=cos⁡αcos⁡α−cos⁡2α−cos⁡2ϕcos⁡α+cos⁡2α−cos⁡2ϕK_a = \cos\alpha \frac{\cos\alpha - \sqrt{\cos^2\alpha - \cos^2\phi}}{\cos\alpha + \sqrt{\cos^2\alpha - \cos^2\phi}} Kp=cos⁡αcos⁡α+cos⁡2α−cos⁡2ϕcos⁡α−cos⁡2α−cos⁡2ϕK_p = \cos\alpha \frac{\cos\alpha + \sqrt{\cos^2\alpha - \cos^2\phi}}{\cos\alpha - \sqrt{\cos^2\alpha - \cos^2\phi}}

Siendo α\alpha la inclinación de la superficie del relleno.

Distribución del empuje activo con relleno inclinado

Teoría de empuje lateral del suelo de Coulomb

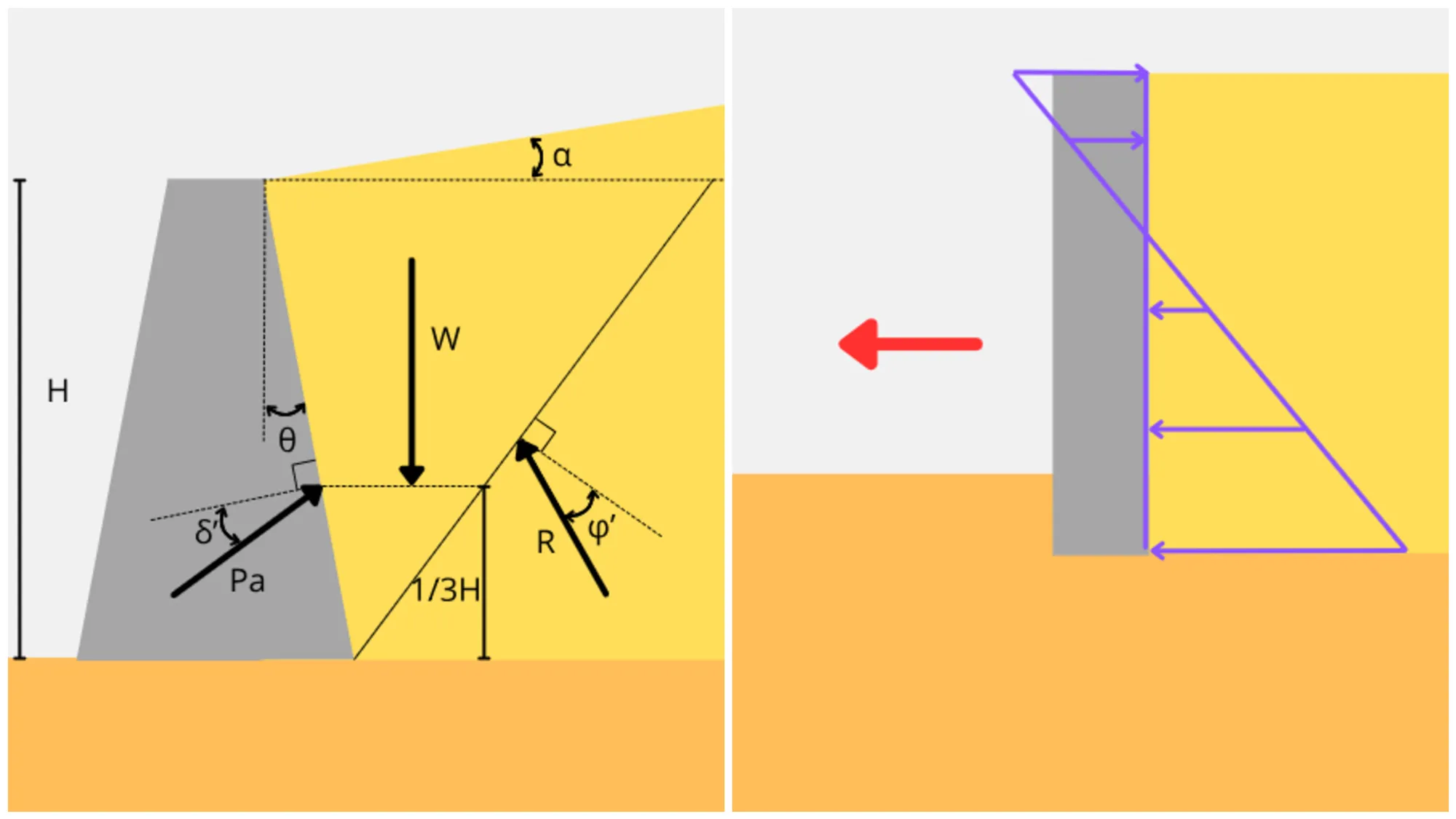
En 1776, el físico francés Charles-Augustin de Coulomb presentó su teoría para determinar las fuerzas activas y pasivas del suelo sobre un muro de contención. Esta teoría toma en cuenta varios factores, como:

  • Inclinación del relleno
  • Inclinación del respaldo del muro
  • Fricción entre el relleno y el muro de contención

Es importante destacar que la teoría de Coulomb solo es aplicable a suelos sin cohesión (c=0)(c = 0). Su desarrollo se basa en el equilibrio de fuerzas y no en el círculo de Mohr.

Dado que la teoría de Coulomb se fundamenta en el equilibrio de fuerzas, proporciona únicamente las fuerzas resultantes del empuje activo y pasivo del suelo, pero no la distribución de presiones a lo largo de la profundidad.

Formulación del empuje de Coulomb

El empuje activo se define como:

Pa=12γH2KaP_a = \frac{1}{2} \gamma H^2 K_a

Donde:

  • PaP_a es la resultante del empuje activo.
  • γ\gamma es el peso específico del relleno.
  • HH es la altura del relleno.

Por su parte, el coeficiente de empuje activo es:

Ka=sin⁡2(ϕ′+β)sin⁡2βsin⁡(β−δ)[1+sin⁡(ϕ′+δ′)sin⁡(ϕ′−α)sin⁡(β−δ′)sin⁡(α+β)]2K_a = \frac{\sin^2(\phi' + \beta)}{\sin^2\beta \sin(\beta - \delta) \left[1+\sqrt{\frac{\sin(\phi' + \delta')\sin(\phi'-\alpha)}{\sin(\beta-\delta')\sin(\alpha + \beta)}}\right]^2}

Donde:

  • β\beta es el ángulo de la cara posterior del muro con respecto a la horizontal.
  • δ′\delta' es el ángulo de fricción entre el suelo y la cara posterior del muro. Usualmente se define como δ′=23ϕ′\delta' = \frac{2}{3}\phi'

Por otro lado, el empuje pasivo se define como:

Pp=12γH2KpP_p = \frac{1}{2} \gamma H^2 K_p

Donde:

  • PpP_p es la resultante del empuje pasivo.

Y el coeficiente de empuje pasivo:

Kp=sin⁡2(β−ϕ′)sin⁡2βsin⁡(β+δ)[1−sin⁡(ϕ′+δ′)sin⁡(ϕ′+α)sin⁡(β+δ′)sin⁡(α+β)]2K_p = \frac{\sin^2( \beta -\phi')}{\sin^2\beta \sin(\beta + \delta) \left[1-\sqrt{\frac{\sin(\phi' + \delta')\sin(\phi'+\alpha)}{\sin(\beta+\delta')\sin(\alpha + \beta)}}\right]^2}

¿Cuál se recomienda utilizar?

La teoría más recomendada y utilizada es la teoría de Rankine, ya que tiene en cuenta factores como la cohesión, y es mucho más flexible ya que al estar basada en el cálculo del esfuerzo efectivo, es más fácil incluir sobrecargas o múltiples tipos de suelo en el relleno.

Ejemplo de cálculo comparativo

Considera el muro presentado en la figura. Calcula el empuje activo utilizando la teoría de Rankine y la teoría de Coulomb.

Ejemplo de cálculo del empuje activo

Teoría de Rankine

Primero se debe calcular el coeficiente de empuje activo.

Ka=cos⁡αcos⁡α−cos⁡2α−cos⁡2ϕcos⁡α+cos⁡2α−cos⁡2ϕ=cos⁡10°cos⁡10°−cos⁡210°−cos⁡230°cos⁡10°+cos⁡210°−cos⁡230°=0.355\begin{aligned} K_a &= \cos\alpha \frac{\cos\alpha - \sqrt{\cos^2\alpha - \cos^2\phi}}{\cos\alpha + \sqrt{\cos^2\alpha - \cos^2\phi}} \\ &= \cos 10° \frac{\cos 10° - \sqrt{\cos^2 10° - \cos^2 30°}}{\cos 10° + \sqrt{\cos^2 10° - \cos^2 30°}} \\ &= 0.355 \end{aligned}

Ahora,al no haber sobrecargas en la superficie del relleno, se procede a calcular el esfuerzo activo en la base del muro.

σ0′=H⋅γ=3⋅18=54kPa\begin{aligned} \sigma'_0 &= H \cdot \gamma \\ &= 3 \cdot 18 \\ &= 54 \text{kPa} \end{aligned}

Con este valor, y al tratarse de un relleno sin cohesión, calculamos el empuje activo.

σa′=σ0′⋅Ka=54⋅0.355=19.17kPa\begin{aligned} \sigma'_a &= \sigma'_0 \cdot K_a \\ &= 54 \cdot 0.355 \\ &= 19.17 \text{kPa} \end{aligned}

Con este cálculo ya podemos calcular la resultante del empuje lateral del suelo.

Pa=12σa′⋅H=1219.17⋅3=28.75kN\begin{aligned} P_a &= \frac{1}{2} \sigma'_a \cdot H \\ &= \frac{1}{2} 19.17 \cdot 3 \\ &= 28.75 \text{kN} \end{aligned}

Teoría de Coulomb

Empezamos calculando el coeficiente de empuje activo del suelo.

Ka=sin⁡2(ϕ′+β)sin⁡2βsin⁡(β−δ)[1+sin⁡(ϕ′+δ′)sin⁡(ϕ′−α)sin⁡(β−δ′)sin⁡(α+β)]2=sin⁡2(30°+90°)sin⁡290°sin⁡(90°−10°)[1+sin⁡(30°+10°′)sin⁡(30°−α)sin⁡(90°−10°′)sin⁡(α+90°)]2=0.341\begin{aligned} K_a &= \frac{\sin^2(\phi' + \beta)}{\sin^2\beta \sin(\beta - \delta) \left[1+\sqrt{\frac{\sin(\phi' + \delta')\sin(\phi'-\alpha)}{\sin(\beta-\delta')\sin(\alpha + \beta)}}\right]^2} \\ &= \frac{\sin^2(30° + 90°)}{\sin^2 90° \sin(90° - 10°) \left[1+\sqrt{\frac{\sin(30° + 10°')\sin(30°-\alpha)}{\sin(90°-10°')\sin(\alpha + 90°)}}\right]^2} \\ &= 0.341 \end{aligned}

Y posteriormente calculamos el empuje activo del suelo:

Pa=12γH2Ka=1218320.341=27.62kN\begin{aligned} P_a &= \frac{1}{2} \gamma H^2 K_a \\ &= \frac{1}{2} 18 3^2 0.341 \\ &= 27.62 \text{kN} \end{aligned}

¿Cómo Diseñar un Muro de Contención con Rischio.io?

El diseño de un muro de contención debe considerar múltiples variables. Rischio.io ofrece una herramienta especializada que permite calcular y analizar muros de contención de manera precisa, mostrando todos los parámetros de diseño y optimización.

¡Prueba ahora nuestra plataforma! Regístrate gratis y obtén cálculos confiables para tus proyectos de ingeniería civil.

Referencias

  • Das, B. M., & Sivakugan, N. (2018). Principles of Foundation Engineering.
Volver a todas las entradas